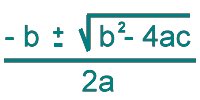Quadratic Equations

Any equation expressible of the form ax² + bx + c = 0 where a is not equal to zero is a quadratic equation in x. A quadratic equation in x is an equation in which the highest power of x is the second power. If an equation is in the form given above, that is if it is written where all nonzero terms are on one side and zero is on the other side, then the quadratic is in standard form.

Methods of Solving Quadratic Equations:

Factoring (Works on some but not all quadratic equations.)
Extraction of Roots (Works on quadratic equations with no first degree term.)
Completing the Square (Works for any quadratic equation.)
Quadratic Formula (Works for any quadratic equation.)

Solving Quadratics by Factoring

Theorem: If ab = 0 either a = 0 or b = 0.

The above theorem is the basis for solving quadratic equations by factoring.

To solve a quadratic equation by factoring

Write the quadratic equation in standard from.
Factor the nonzero side of the equation. (Remember not all quadratics factor.)
Set factors equal to zero.
Solve the two linear equations obtained in the step above.

Examples:

x² = 4 Write in standard form. x² - 4 = 0. Factor left side. (x = 2)(x - 2) = 0 Set factors equal to zero. x + 2 = 0 or x - 2 = 0 Solve the equations. x = -2 or x = 2 Express results as a solution set. {-2,2}
x² - 8x = -16 Write in standard form. x² - 8x + 16 = 0 Factor left side. (x - 4)(x - 4) = 0 Set factors equal to zero. x - 4 = 0 or x - 4 = 0 Solve the equations. x = 4 or x = 4 Express results as a solution set. {4} Note there is only one distinct solution.
10x² + 5x = 30 Write in standard from. 10x² +5x - 30 = 0. Factor left side. 5(2x² + x - 6) = 0 Continue factoring left side. 5(2x - 3)(x + 2) = 0 Set factors equal to zero. Note first factor can not equal zero. 2x - 3 = 0 or x + 2 = 0 Solve the equations. 2x = 3 or x = -2 x = 3/2 or x = - 2 Express answer as a solution set. {3/2, -2}

A solution to an equation is also called a root of the equation. Every quadratic equation has two solutions or roots. The roots may or may not be distinct. In the second example four is called a double root of the equation or a root of multiplicity two since both roots of the equation are one and the same.

Solving Quadratics by Extraction of Roots

A quadratic equation with no first degree term can be solved easily by the extraction of roots method.

To solve a quadratic by the extraction of roots method:

Isolate second degree term on one side of the equation.
If coefficient of second degree term is not one, divide both sides by the coefficient
Take square root of both sides of the equation. Remember every nonzero real number has two square roots over the Complex field.

Examples:

x² - 36 = 0

x² = 36 (Isolate variable)

x = ± 6 (Extract roots.)

3x² - 125 = 0

3x² = 75 (Isolate variable)

x² = 25 (Divide by 3)

x = ± 5 (Extract roots.)

Solving Quadratics by Completing the Square

Remark: Solving quadratic equations by completing the square is a generalization of solving quadratic equations by the extraction of roots method.

To solve a quadratic equation in a single variable x by completing the square:

Isolate the terms involving the x on one side of the equation, constant on the other side.
If coefficient of second degree term is not one, divide each side of the equation by the coefficient of second degree term.
Complete the square. This is accomplished by adding the square of 1/2 of the coefficient of the first degree term to each side of the equation.
Factor the perfect square trinomial thus obtained and combine constants on other side of the equation.
Extract roots.
Solve for x.

Example:

2x² - 6x + 5 = 0

2x² - 6x = - 5 (Isolate variable)

x² - 3x = - 5/2 (Divide by coefficient of second degree term)

x² - 3x + 9/4 = - 5/2 + 9/4 (Complete the square)

(x - 3/2)² = -1/4 (Factor perfect square trinomial and combine constants.

(x - 3/2) = + or - i/2 (Extract roots.)

Solving Quadratics Using the Quadratic Formula

The roots of the quadratic ax² + bx + c = 0 are given by

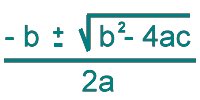
To solve a quadratic using the quadratic formula

Write in the form ax² + bx + c = 0. That is, write in standard form.
Determine a, b, and c. the coefficients of the second degree term, the first degree term, and the constant term respectively.
Substitute into the formula.
Simplify radican first, then radical if possible, and lastly reduce fraction if possible. Remember to reduce a fraction the numerator must be in factored form!

Example:

3x² + 4x = 2

3x² + 4x - 2 = 0 (Write in standard form.)

a = 3, b = 4, c = -2

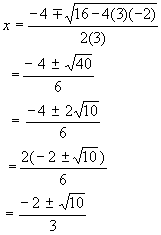
Go back to equations menu.

Go back to tutorial menu.

Go back to home page.