Simplifying Radical Expressions I

A radical expression is not in simplest or stanedard form if radicand contains a factor raised to a power greater than or equal to the index of the radical.
1. To see whether or not a radical will simplify we factor the radicand as a product of prime factors.
2. Write the radicand as a product of two sets of factors. The first set of factors should have exponents which are divisible by the index of the radical, the second set should have exponents less than the index of the radical.
3. Use property II to write the radical as a product of two radicals.
II. Product Property
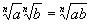
4. Use property I to simplify first radical.
I. If n is even
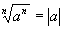
if n is odd
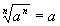
Examples:
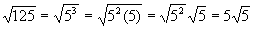
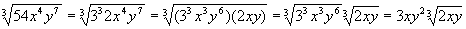
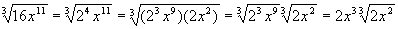
Copyright © 1995 - Present. SSmyrl
![]()
![]()
![]()
![]()
![]()
![]()