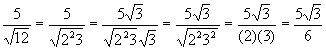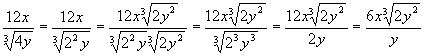Simplifying Radical Expressions II

A radical expression is not in simplest or
standard form if there is a radical in the denominator. To simplify the
expression we ratioalize the denominator.
A. Monomial Denominator
1. To simplify factor radicand as a product
of prime factors.
2. Multiply numerator and denominator by
radical whose order is the same as the order of radical in the denominator. The
radicand is chosen so that the product of the original radicand and radicand of
multiplier will give exponents which are divisible by index. Factors in
radicand of multiplier should all have exponents less than index of radical.
3. Use property II to multiply radicals
together.
II. Product Property
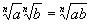
4. Use property I to simplify radical(s).
I. If n is even
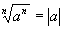
if n is odd
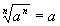
Examples:
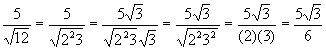
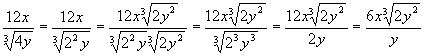
B. Binomial Denominator
To simplify a radical expression with one
or two second order radicals in a binomial denominator, multiply numerator and
denominator by the conjugate of the denominator. Remember the conjugate of a +
b is a - b and the conjugate of a - b is a + b.
Exam
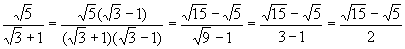
Copyright © 1995 - Present. SSmyrl
|