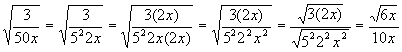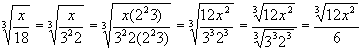Simplifying Radical Expressions III

A radical expression is not in
simplest or standard form if radicand is fractional
To simplify:
1. Factor the denominator of the
fraction as a product of primes.
2. Use fundamental theorem of
fractions to write the fractional radicand as an equivelent
fraction where all prime factors in denominator are divisible by
index of radical. This is accomplished by multiplying numerator
and denominator of the fraction by prime factors all with
exponents less than the index.
3. Use property III to write the radical
as a quotient of two radicals.
Property III:
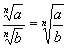
4. Use property I to simplify the radical
in the denominator
I. If n is even
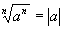
if n is odd
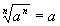
Examples:
Assume all variables are positive. (Error
on last example. I have no equation editor to correct.)
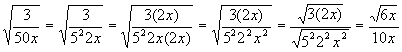
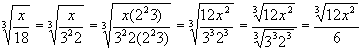
Copyright © 1995 - Present. SSmyrl
|